Contact Mechanics

Contact detection algorithm

The contact algorithms in OpenFDEM is divided into: (a) neighbour search and (b) geometric resolution. Neighbour search is a rough search aims to provide a list of possible blocks in contact including global search e.g. an altering digital tree (ADT), no binary search (NBS) contact detection algorithm, CGRID, DESS algorithm, master-slave algorithm and local search, e.g. node-to-surface (NTS) algorithm, RIGID algorithm, inside-outside algorithm. Geometric resolution algorithms strongly depend on complexity of the geometric representation of cells. The discrete function representation (DFR) algorithm has a computational complexity of order O(N) and the common-plane (CP), which bisects the space between two contacting blocks, is advantageous for vertex-to-vertex or edge-to-vertex contacts where the definition of the contact normal is a non-trivial problem and the method has a complexity of order O(N). The number of iterations of CP is depended on the accuracy of the initial guess of the CP position, and then a fast common plane (FCP) method and a shortest link (SL) method are proposed to increase efficiency of the CP method.

In OpenFDEM, the contact detection algorithm is developed for blocks with evident size using square bounding box method in cooperation with the NBS algorithm (shown in Figure 1), which aims to divide the NBS model to several groups (list in Table 1), the flow chart of the enhanced NBS algorithm is

\[{{\mathbf{x}}}^{k} = 1 + int\left( \frac{{{\mathbf{x}}}_{i} - {{\mathbf{x}}}_{\min}}{d(0)}\ + \ \frac{1}{2} \right) \tag{1}\]

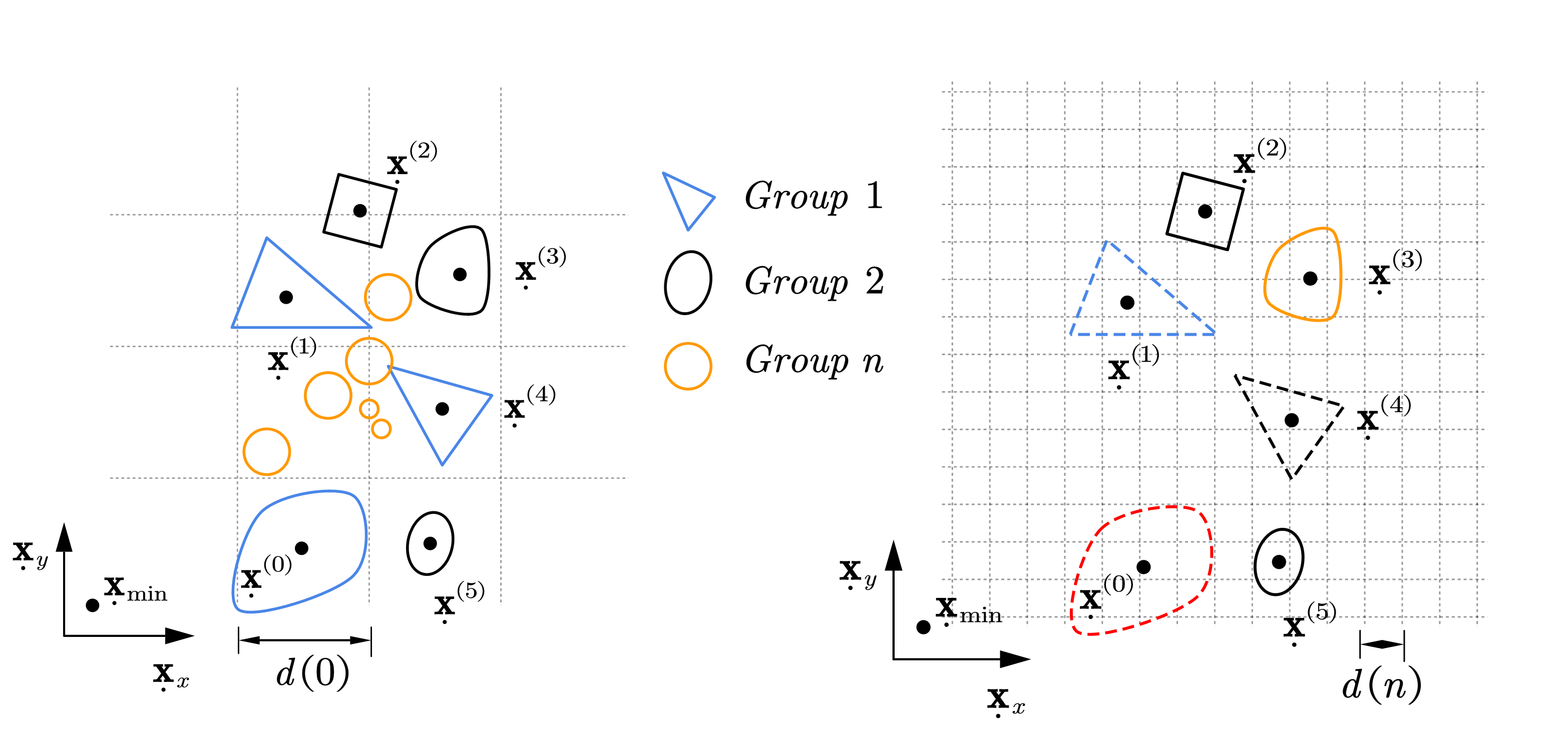
Figure 1. The schematic algorithm of NBS contact detection in OpenFDEM.

The enhanced NBS contact detection method used in mGbCDM

Table 1

Step 1: Loop the blocks and find the maximum size buffer box for the initial group box \(d(0) = d_{\max}\);

Step 2: Divide the blocks into \(n\) groups with size of buffer box for the nth group box as \(d(n) = d_{\max} \cdot \alpha^{n - 1}\), \(\alpha \in \left( 0\ ,\ \left. \ 1 \right\rbrack \right.\ \);

Step 3: All the blocks are mapped in to the grid space with edge length of \(d(0)\) as depicted in Figure 2 , the central point of the block \({\underset{˙}{\mathbf{x}}}^{k}\) is computed in Eq ;

Step 4: Loop all the blocks and detect contacts for the first group, the contact couple groups is identified when \(\left| {\underset{˙}{\mathbf{x}}}^{(t)}\ - \ {\underset{˙}{\m athbf{x}}}^{(c)} \right| < \max\left( d^{(t)}\ + \ d^{(c)} \right)\), the contact state can be recognized as neighboring contacts or center contacts;

Step 5: Repeat step 3 and step 4 for all groups of the remaining blocks and identify the states of the contacts;